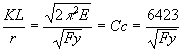4.- MIEMBROS SUJETOS A COMPRESIÓN
Los miembros sujetos a compresión se distinguen de los sujetos a tensión por lo siguiente:
- Las cargas de tensión tienden a mantener rectos a los miembros mientras que las de compresión tienden a flexionarlas.
- La presencia de agujeros en la sección transversal de miembros reducen el área efectiva de tensión, mientras que en el caso de compresión, los tornillos, remaches y pernos llenan al agujero apoyándose en ellas a pesar la holgura que existe considerando las áreas totales disponibles para soportar la compresión.
La experiencia demuestra que mientras las columnas son lo suficientemente cortas, falla plastificándose totalmente todas las "fibras" de la sección transversal (es decir que alcanzan el esfuerzo de fluencia), que es el límite elástico del material (Fy).
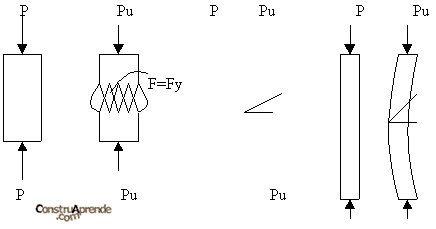
Conforme aumentan su longitud sin variar su sección transversal, las columnas fallan alcanzando el esfuerzo de fluencia solo algunas "fibras de la sección", llamadas columnas intermedias. Finalmente cuando las columnas son lo suficientemente largas fallan sin que ningún punto alcance el valor del esfuerzo de fluencia.
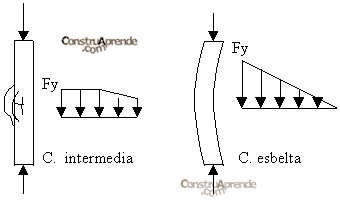
En 1757 Leonhard Euler (suizo) desarrollo un modelo matemático para descubrir el comportamiento de las columnas esbeltas de la manera siguiente:
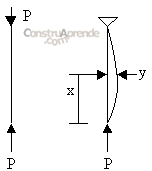
La ecuación de curvatura para una barra en flexión: 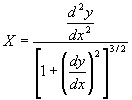 si dy/dx » 0 x = d2y/dx2
si dy/dx » 0 x = d2y/dx2
De resistencia de materiales se tiene:
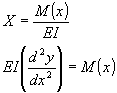
Para nuestro caso: ![]()
Ecuación asociada: ![]()
de donde: ![]()
para las condiciones de frontera: 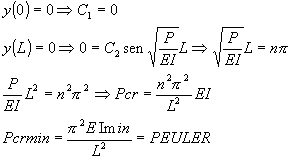
como I = Ar2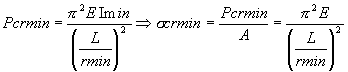
Ec. Para carga mínima crítica de pandeo de columna esbelta de Euler
Para obtener la sección transversal mínima que garantice alcanzar el esfuerzo de fluencia:
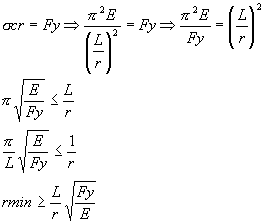
Las pruebas hechas en columnas producen valores de relaciones de esbeltez distribuidos en una franja ancha que promedia la curva de comportamiento real de falla de las columnas.
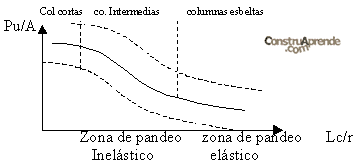
Los factores que afectan la resistencia de las columnas son varias aún en condiciones de laboratorio:
- Centrado de la energía
- Imperfecciones de la sección
- Homogeneidad del material
- Rectitud del elemento columna
- Esfuerzos residuales
Las condiciones de apoyo son las más importantes a menudo para determinar la carga crítica de una columna, debido a la variación de casos que se presentan en la práctica, por lo cual se ha considerado en la fórmula de Euler el valor de L como la "longitud efectiva" de la columna, es decir, la longitud entre puntos de inflexión en la geometría deformada de la columna considerando un valor de k de modo que el producto kL = Le = longitud efectiva de la columna.
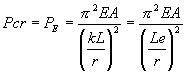
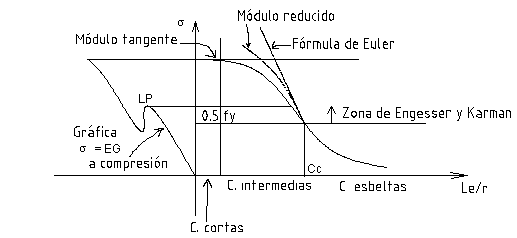
La fórmula de Euler solo predice el comportamiento en columnas esbeltaz, cuando "L" es la longitud efectiva de la columna, sin embargo cuando el esfuerzo es próximo al límite de proporcionalidad del material se separa la función de Euler del comportamiento real; al límite de la relación de esbeltez a partir del cual esta sucede se le denomina Cc y comienza el comportamiento inelástico que fue estudiado por Engesser y Karman proponiendo fórmulas para el módulo secante y módulo reducido las cuales aún se encuentran en discusión pero obtienen valores cercanos al comportamiento real.
![]()
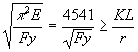
FORMULA DEL MÓDULO SECANTE
Para determinar el esfuerzo máximo para la zona inelástica de pandeo, se obtiene aproximadamente como:
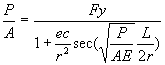
donde:
Fy = Límite de fluencia del acero
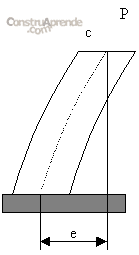
e = Excentricidad de la carga aplicada
c = Distancia del centroide a la fibra más alejada
![]() = Relación de excentricidad
= Relación de excentricidad
Esta ecuación considera esfuerzos secundarios debidos a flexión y curvado inicial de las columnas.
El problema de resolver esta ecuación, es que el valor a obtener P/A está implícito, de forma que se obtiene mediante iteraciones sucesivas.
Para este caso, se considera como límite superior del comportamiento elástico 0.5 Fy, de tal forma que:
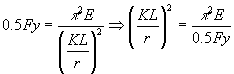
|
 |
DISEÑO DE MIEMBROS A COMPRESIÓN
NTC – Estructuras metálicas:
Para secciones 1,2 y 3 se considerará el estado límite de inestabilidad por flexión.
Para secciones 4 además se considerará el estado límite de pandeo local.
En algunos casos de secciones con uno o con ningún eje de simetría (LI, TR, CE) y con dos ejes de simetría pero baja rigidez torsional (IE, IR, IS) se deberán considerar también los estados límite de pandeo por flexotorsión.
ESTADO LIMITE DE PANDEO POR FLEXIÓN:
- Miembros IE, IR, IS, PTR y semejantes:
- Miembros de sección cualquiera en a)
donde:
Fr = 0.9 ![]()
IR, IS, IE, PTR y las formadas por cuatro placas soldadas tipo 1, 2, 3 implican que n=1.4
IR, IS, IE formadas por tres placas soldadas tipo 1, 2, 3 implican n = 1.0
Si 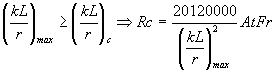
Si 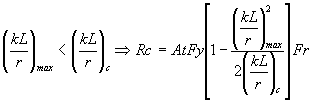
Donde:
Fr = 0.85
![]() (relación de esbeltez que separa los rangos de columnas esbeltas de las intermedias)
(relación de esbeltez que separa los rangos de columnas esbeltas de las intermedias)
![]() máxima relación de esbeltez de la columna
máxima relación de esbeltez de la columna
ESTADO LIMITE DE PANDEO LOCAL
Para secciones tipo 4, sin importar la forma de la sección transversal, la resistencia a compresión Rc se determina como:
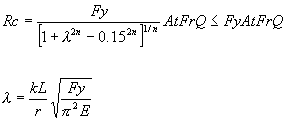
donde:
n = según se especificó antes
Fr = 0.9
Q = factor de pandeo local = QsQa
Qs = correspondiente al elemento plano no atiesado con el mayor valor b/t
- En secciones formadas únicamente por elementos planos atiesados Qs = 1
- En secciones formadas únicamente por elementos planos no atiesados Qa = 1
Para secciones OC tipo 4 y D/t < 914000/Fy se tomará el menor de los siguientes valores:
![]()
y de:
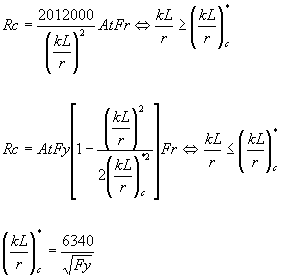
Fr = 0.70
Nota: En todos los casos la relación de esbeltez a compresión (KL/r)max < 200
ESTADO LIMITE DE PANDEO POR FLEXOCOMPRESION
En miembros comprimidos con uno o ningún eje de simetría, tales como LI, LD, TR o con dos ejes de simetría pero muy baja rigidez torsional: IE, IR, IS, secciones en cruz, puede ser necesario revisar los estados límite de pandeo por flexotorsión o torsión, cuyos procedimientos no están incluidos en estas normas:
Consultar : Vasili Ilich Vlasov: Secciones de pared delgada.