54 CommentsDISEÑO DE MIEMBROS SUJETOS A TENSIÓN.
NTC-METALICAS:
Para el diseño de miembros a tensión de acuerdo a las NTC se consideran dos estados que son:
- Estado límite de flujo plástico en la sección total (para limitar la elongación del miembro):
- Estado límite de fractura en la sección total:
Rt = Fr Fy At
Fr = 0.9
Fr = 0.75
Donde:
Fr = factor de resistencia
Rt = resistencia a tensión del miembro (kgf)
At = área total de la sección (cm2)
Ae = área neta efectiva de la sección (cm2)
Fy = esfuerzo de fluencia del acero empleado(kgf/cm2)
Fu = esfuerzo último (de ruptura) del acero (kgf/cm2) a tensión.
En miembros sin agujeros conectados mediante soldaduras colocadas en todos los elementos que componen su sección transversal, se tomará Ae = At.
Si existen agujeros entre las conexiones soldadas de los extremos del elemento, o bien si contienen soldaduras de tapón o ranura se empleará el área neta efectiva a través de los agujeros.
- Calcular el área mínima efectiva y total necesaria para una placa prismática, que deberá soportar una tensión de 10 ton por CM + CV, si pertenece a una estructura tipo B, acero A-36.
| 1.4(10000 kg) < |  |
|
- 14000 kg <= 0.9 (2530 kg/cm2) At
- 14000 kg < 0.75(4080 kg/cm2) Ae
At >= 6.15 cm2
|
|
|
At > 6.15 cm2
(a) flujo plástico
0.80 At > 4.58 cm2
At > 5.75 cm2(b)
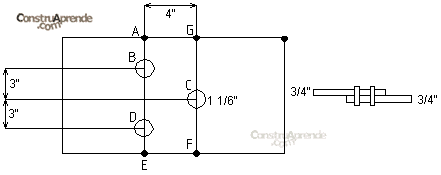
- Determinar el área total necesaria para una placa sujeta a tensión que soportara 5 ton po (CM + CV + V) si será conectada de la manera siguiente.
Fy = 2950 kg/cm2
Fu = 4430 kg/cm2
| 1.1 (1500 kg)< | |
|
| 16500 < 2655At | At > 6.21 cm2 ............1 |
| 16500 < 3322.5 Ae | Ae > 4.97 cm2.............2 |
| At = 1.9 b = 6.21 | b > 3.27 cm ................1 |
- ABDE
- ABCDE
- ABCF
- GCF
| b - 2.70 | be = b – 5.40 | Ae = 1.9 (b-5.40) | 1.9 (b - 5.40) > 4.97 .........2 |
b > 8.01 cm ........2 Falla por fractura en la sección
At = (1.9) (26.04) At = 49.47 cm2
Ae = be h be = 26.04 – (2.70)2 be = 20.64 cm
Ae = 1.9 (20.64) Ae = 39.21 cm2
U = 0.79 Para saber que tan óptima es la sección
BLOQUE DE CORTANTE (INTERACCIÓN – TENSIÓN – CORTANTE)
La resistencia de diseño de un miembro a tensión, no siempre esta gobernada por las expresiones que consideran la falla por fractura o por flujo plástico, ni por la resistencia de los tornillos, remaches o soldaduras; si no que también a veces depende de la resistencia de su "bloque de cortante" que es la zona de conexión del miembro, definida por un plano de falla a cortante y uno transversal a tensión.
En este caso de la falla de los planos no ocurre simultáneamente pudiendo presentarse dos casos:
CASO A:Área grande a cortante y área pequeña a tensión:
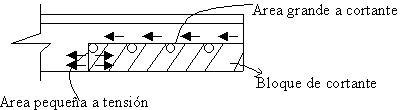
Cuando se tiene un área grande a cortante y una pequeña a tensión su resistencia será a cortante y no a tensión, por lo que primero se presentará el flujo del área a tensión y la falla después a cortante, a este caso se le denomina fluencia por tensión y fractura por cortante, y su resistencia se determina como:
AgtFy = fluencia por tensión
0.6AncFu = fractura por cortante
CASO B:Area grande a tensión y área pequeña a cortante:
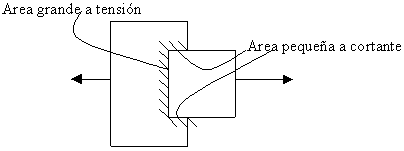
Para este caso la resistencia será a tensión y no a cortante de modo que primero se presentará la fluencia a cortante y luego la fractura a tensión denominándole fractura por tensión y fluencia por cortante:
AntFu = fractura por tensión
0.6AgvFy = fluencia por cortante
donde:
Agu = área total sujeta a cortante
Fr = 0.75
Agt = área total sujeta a tensión
Anv = área neta sujeta a cortante
Ant = área neta sujeta a tensión
Agv = área total sujeta a cortante
Rtb = resistencia total sujeta a cortante
Fu = esfuerzo último del material
La resistencia total del bloque de cortante Rtb, se determina como la menor de las dos expresiones calculadas de Rtb.
Nota: deberán aplicarse ambas ecuaciones, a fin de determinar el tipo de falla. Rigiendo la que de la menor resistencia (se escoge la menor).
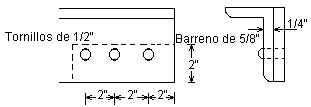
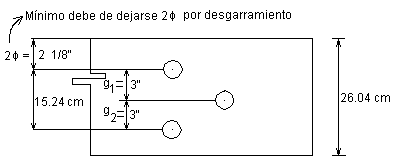
Determinar la resistencia del bloque de cortante para la fig. ilustrada.
A – 36 Fy = 2530 kg/cm2 Fu = 4080 kg/cm2
Agt = 5.08 (0.63) = 3.20 cm2 Ant = 3.20 cm2
Agv = (0.79 + 15.24) (0.635) = 10.09 cm2 Anv = 10.09 cm2
se escoge esta
