En la tabla 4.2.1.1 se presentan los periodos de vibración de cada modelo.
|
Modelo |
Periodo (s.) |
||
|
Modo 1 |
Modo 2 |
Modo 3 |
|
|
Biggs |
0.754 |
0.260 |
0.178 |
|
B1 |
0.998 |
0.277 |
0.179 |
|
B2 |
0.844 |
0.309 |
0.190 |
|
B3 |
0.766 |
0.309 |
0.209 |
|
B4 |
1.059 |
0.348 |
0.190 |
|
B5 |
1.004 |
0.326 |
0.214 |
|
B6 |
0.855 |
0.329 |
0.249 |
|
B7 |
1.551 |
0.376 |
0.190 |
|
B8 |
1.518 |
0.338 |
0.216 |
|
B9 |
1.104 |
0.371 |
0.271 |
|
B10 |
1.249 |
0.456 |
0.195 |
|
B11 |
1.031 |
0.469 |
0.229 |
|
B12 |
0.898 |
0.437 |
0.283 |
Tabla 4.2.1.1 Periodos de vibración de los casos estudiados para el modelo de cortante de Biggs
Con el fin de hacer más evidentes los resultados obtenidos se presentan gráficas en las cuales se emplea un índice definido como error relativo. En las figuras 4.2.1.2. a la 4.2.1.4., se presentan, en el eje horizontal el número de modo de vibrar, y en el vertical, el valor absoluto del error relativo (en porcentaje) detectado en con los métodos MAC, IMAC y POC. Cada una de las figuras corresponde a un término de la diagonal de la matriz de correlación obtenida de la aplicación de los métodos, que miden la correlación entre los tres vectores modales calculados.
En estas gráficas se presentan los doce casos de daño estudiados. En ellas se puede observar cuál modo de vibrar es el más afectado, para cada uno de los casos de daño.
Para el criterio MAC, figura 4.2.1.2., para el primer modo el caso más severo es el B9, para el segundo y tercer modo es el B12; y se tiene el tercer modo el valor máximo es 46% de error. En el criterio IMAC, figura 4.2.1.3., para el primer el caso más severo es el B9, para el segundo modo es el B12 y para el tercero es el B11; y se tiene al segundo modo como el más afectado con un 76% de error. Para el POC, figura 4.2.1.4., se tiene para el primer al B9 como el caso más severo, para el segundo y tercer modo se tiene al caso B11 como el más severo; y el segundo y tercer modo resultan ser los afectados con un error de cerca del 80%. Estos criterios sirven para identificar a los casos de daño más severos, entre ellos.
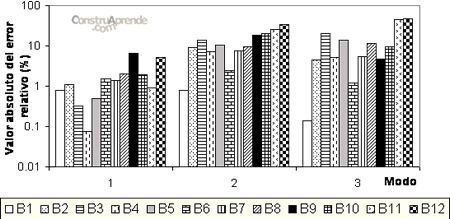
Fig. 4.2.1.2. Error relativo en % de los doce casos de daño utilizando el criterio MAC.
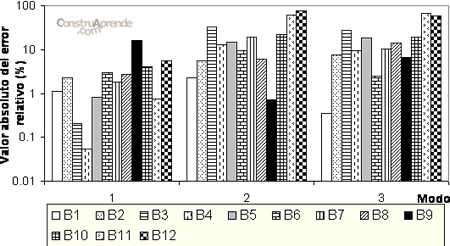
Fig. 4.2.1.3. Error relativo en % de los doce casos de daño utilizando el criterio IMAC.
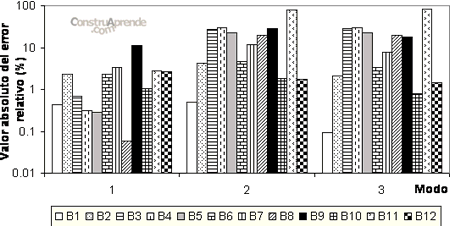
Fig. 4.2.1.4. Error relativo en % de los doce casos de daño utilizando el criterio POC.
En las figuras 4.2.1.5. y 4.2.1.6. se presentan los resultados, como errores relativos para cada uno de los entrepisos del marco, de los criterios CoMAC y ECoMAC. En ellas, en el eje horizontal se presentan los valores absolutos del error relativo (en porcentaje) y en el eje vertical los entrepisos del marco; a diferencia de los métodos anteriores, éstos dos proporcionan información sobre la detección de daño en cada uno de los entrepisos. En estas gráficas se puede apreciar qué entrepiso se detecta como el más dañado.
El método CoMAC detecta adecuadamente los casos B3, B5, B7, B8 y B11; para los cuales identifica los entrepisos con daño (aunque no en todos los casos se refleja el porcentaje de daño entre uno y otro) y muestra que el modelo con el daño más severo, cualitativamente, es el caso B12. El método ECoMAC detecta adecuadamente los casos B1, B3, B5, B8 y B11 y muestra que, cualitativamente, el caso con el daño más severo es el B11.
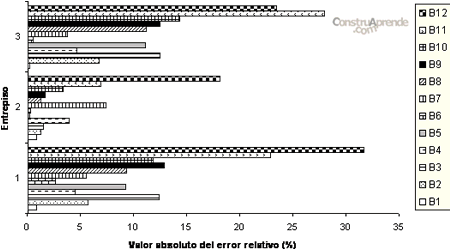
Fig. 4.2.1.5 Error relativo en % de los doce casos de daño utilizando el criterio CoMAC
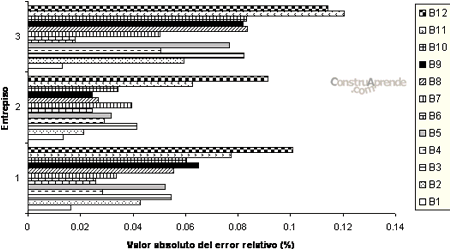
Fig. 4.2.1.6 Error relativo en % de los doce casos de daño utilizando el criterio ECoMAC

