El objetivo básico en el modelaje analítico de la estructura de un puente es proveer la formulación matemática más simple del comportamiento de la estructura que satisfaga un particular diseño para determinar la respuesta de la misma. Aceptando que se cuenta con las herramientas analíticas apropiadas para llevar a cabo el análisis, el modelo debe reflejar las interacciones físicas propias de la estructura con las solicitaciones a que estará expuesta.
El modelo debe describir la geometría, la masa, las condiciones de conectividad y restricciones, así como las cargas lo más cerca de la realidad que sea posible para facilitar la interpretación de la respuesta. Elementos individuales simulando partes de la estructura o componentes completos del puente son conectados mediante nodos y los desplazamientos nodales son usados como incógnitas o grados de libertad en el análisis.
En adición al modelaje de la geometría y la caracterización de las cargas inducidas a los elementos, la masa asociada a cada grado de libertad debe determinarse, ya que, las fuerzas de inercia contribuyen a la respuesta del puente. Además, las conexiones entre los marcos individuales del puente, los apoyos y la cimentación son complejas y típicamente se hacen simplificaciones en el modelaje.
La mejor descripción de la geometría del puente en estudio debe comprender un modelo de cada uno de los elementos estructurales y que represente su relación física y de espacio con otros elementos, pero esto no es siempre posible porque existen puentes que están formados de armaduras, las cuales a su vez están formadas por elementos, así como las conexiones entre cada armadura está compuesta de varios elementos; una discretización detallada de cada uno de estos elementos estructurales y el modelaje de sus características de conexión y fuerza – desplazamiento es prohibitiva para el sistema total del puente. La necesidad de separar el sistema total en subsistemas manejables, marcos y elementos estructurales individuales para propósitos de modelaje es bastante obvio, y las diferentes opciones de modelaje son expuestas a continuación.
3.3.1 Tipos de modelos analíticos empleados en puentes
El sistema estructural total de un puente consiste en la superestructura, subestructura y cimentación. La superestructura, particularmente para puentes largos, es separada en secciones mediante juntas de expansión que permiten la expansión o contracción del puente sin introducir grandes esfuerzos o deformaciones a elementos individuales, o bien, por juntas de construcción articuladas que forman parte de un sistema particular de construcción. Son importantes estas juntas donde puedan presentarse deformaciones relativas entre partes de la superestructura para su respuesta sísmica, ya que las discontinuidades en el movimiento en éstas permiten que las secciones individuales del puente respondan con diferentes características y con una interacción compleja ante la fuerza inducida, por ejemplo por un sismo.
Junto con sus respectivas subestructuras o sistemas de apoyo, como pilas, columnas y cimientos, estas secciones de la superestructura, referidas como marcos, juegan un rol principal en la cuantificación de la respuesta sísmica, debido a sus características dinámicas de respuesta individuales. La respuesta individual de cada marco está controlada por la masa, y se debe su contribución principalmente a la superestructura. Para reflejar la importancia y diferencias entre estos subsistemas individuales, en términos de la cuantificación de la respuesta sísmica del modelo analítico del puente, se hace una distinción entre (i) modelos globales, (ii) modelos de marcos y (iii) modelos de vigas.
3.3.2 Modelos globales
Los modelos globales de la estructura completa del puente tiene una utilidad limitada, excepto por los casos donde (1) el puente es corto y está formado por un solo marco, (2) la respuesta esperada es en el intervalo elástico, y (3) cuando se pueden establecer las variaciones del movimiento del suelo a lo largo de la longitud total del puente.
Los modelos globales de puentes son empleados predominantemente en la cuantificación de la respuesta sísmica, para determinar desplazamientos elásticos y fuerzas equivalentes en los miembros. Dado que el valor real de modelos analíticos globales radica principalmente en la caracterización del sistema total del puente, éstos deberían emplearse primordialmente al final del diseño sísmico o contribuir al proceso para verificar los parámetros de cada subestructura en el sistema total, lo cual no es considerado en los otros modelos. En la figura 3.5.1. se presenta un modelo global de la estructura de un puente recto.
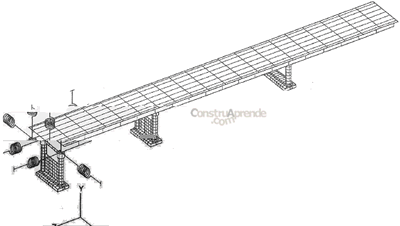
Fig. 3.5.1. Modelo global de la estructura de un puente recto.
3.3.3 Modelos de puentes a base de marcos
Los modelos de puentes a base de marcos individuales proveen una herramienta útil para obtener la respuesta sísmica, dado que las características de la respuesta dinámica de un marco individual puede evaluarse con una precisión razonable. Un análisis con modelos de marcos individuales puede dar un mejor conocimiento de las características de la respuesta individual de las secciones del puente.
La interacción con los marcos adyacentes puede ser considerada en un análisis marco por marco en la forma de resortes, los cuales son típicamente modelados con características elásticas lineales. Otra aproximación comúnmente empleada es la de modelar grupos de marcos; donde tres o cinco marcos son modelados simultáneamente con las apropiadas suposiciones para modelar las características de los movimientos de las juntas, y solo la respuesta resultante del marco interior (o marcos) es considerada como representativa de la contribución en el análisis. En la figura 3.6.1. se presenta un modelo de marcos.
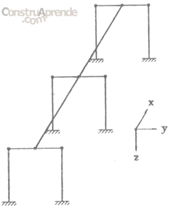
Fig. 3.6.1. Modelo de marcos de la estructura de un puente.
3.3.4 Modelos de vigas
El desarrollo de modelos realistas de marcos requiere una discretización detallada de las vigas que forman la estructura; dado que, generalmente, la rigidez del marco está dada directamente por las vigas. Los modelos de vigas son usados principalmente para determinar la rigidez efectiva. Modelos de vigas deben incluir los efectos de flexibilidad de la cimentación y pueden ser combinados en modelos de marcos como elementos a la mitad de la superestructura. El hecho de que la mayoría de las superestructuras de los puentes presenten una alta rigidez en el plano, permite como una muy buena aproximación, suponer movimientos de cuerpo rígido de la superestructura, lo cual simplifica ampliamente la combinación de modelos de vigas. En la figura 3.7.1. se presenta un modelo de vigas.
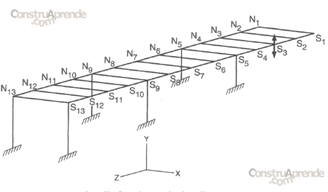
Fig. 3.7.1. Modelo de vigas de la estructura de un puente.
3.3.5 Elementos estructurales
Cualquiera que sea el tipo de modelo que se emplee para representar la estructura de un puente, se utilizan elementos para describir las características del comportamiento físico de elementos entre nodos, definidos en la discretización matemática de la estructura del puente. Los tres grupos de elementos estructurales, que generalmente se emplean en modelos de puentes son (1) elementos lineales, (2) placas y cascarones, y (3) sólidos. Los elementos lineales son de la forma de resortes, elementos viga y barra, empleados principalmente en modelos esqueletales; las placas, cascarones y elementos sólidos se emplean en modelos de elementos finitos.
Los elementos en un modelo analítico están conectados a los nodos definidos en la discretización estructural y son compatibles con la localización de los desplazamientos incógnitas en las que nos interesa conocer la respuesta modal. Diferentes tipos de elementos estructurales se presentan en la figura 3.8.1. Los elementos lineales se representan en la figura 3.8.1.(a) como un elemento viga, con seis grados de libertad en cada nodo (tres giros y tres desplazamientos). Un elemento bidimensional está representado en la figura 3.8.1.(b), con una discretización de cuatro a nueve nodos; mientras que la formulación de cuatro nodos en las esquinas es simple, un número grande elementos o discretización más refinada, con un número mayor de grados de libertad, es necesaria para vencer la limitada flexibilidad en estos elementos; la adición de nodos en el centro y a la mitad de los nodos de las esquinas proveen flexibilidad adicional al modelo; este tipo de elementos tiene sólo dos grados de libertad por nodo (dos desplazamientos). En la figura 3.8.1.(c) se representa un elemento placa; típicamente cada nodo tiene cinco grados de libertad en un elemento placa o cascarón (tres desplazamientos y dos giros). Finalmente, elementos sólidos tridimensionales se muestran esquemáticamente en la figura 3.8.1.(d), en donde se tienen tres grados de libertad por nudo (tres desplazamientos); al igual que en los elementos planos, se pueden emplear un número mayor de nodos de los que se necesitan para modelar cada elemento. Caracterizaciones detalladas de estos elementos están mas allá del alcance de este trabajo y pueden encontrarse en la literatura de análisis estructural general y teoría del elemento finito (Hughes, 1987).
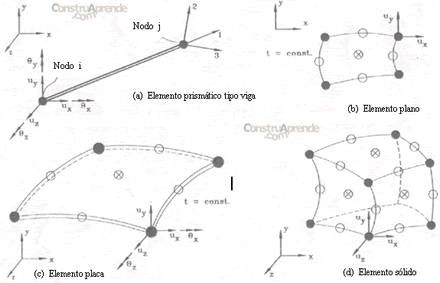
Fig. 3.8.1. Algunos tipos de elementos que se emplean en el modelaje de puentes.
3.3.6 Modelaje de los componentes de la estructura de puentes
En el modelaje de puentes es necesario tomar en cuenta factores tales como: (1) geometría y caracterización efectivas de miembros, (2) definición adecuada de detalles de apoyo y conexiones, y (3) efectos de cargas permanentes y participación de masas. En la mayoría de los puentes, por definición, la longitud grande de los claros, les permite ser considerados como estructuras rectas, donde la longitud del claro L entre apoyos es mayor que el ancho B o el espesor D de la superestructura, como se muestra en la figura 3.9.1. Para el análisis de un puente no es necesario un modelo tridimensional de la superestructura con elementos finitos empleando elementos placa o elementos sólidos; más bien, modelos más simples son suficientes, siempre y cuando estos representen las características de rigidez efectiva y distribución de masa (Farrar et al, 1998).
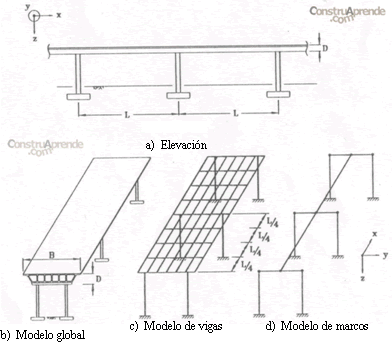
Fig. 3.9.1. Modelos que representan la superestructura de un puente.
En muchos casos, la superestructura de un puente, debido a su rigidez en el plano, puede suponerse que tiene un movimiento de cuerpo rígido bajo la acción de fuerzas sísmicas, y el problema entero del modelaje se reduce a representar la rigidez de los apoyos mediante restricciones en la geometría simulando la rigidez de la superestructura; donde la flexibilidad vertical de la superestructura reduce la unión con las columnas y apoyos.
En casos donde la superestructura no puede considerarse rígida (como por ejemplo, puentes largos y angostos), la superestructura puede ser modelada como una retícula de vigas como se muestra en la figura 3.9.1.(c) o simulando una columna vertebral o espina con elementos tipo viga a lo largo del centro de gravedad de la sección transversal a todo lo largo de la longitud del puente, como se muestra en la figura 3.9.1.(d); Propiedades equivalentes para los miembros de la 'columna vertebral' necesitan ser calculadas, las cuales representarán la rigidez efectiva de la superestructura.
Un modelo del tipo espina o 'columna vertebral' con uniones rígidas en los apoyos no representan adecuadamente la distribución de las cargas gravitacionales hacia las columnas y candeleros, dado que, típicamente, en este tipo de modelos las cargas se aplican a lo largo del eje de la espina.
Un modelo tipo retícula bidimensional es capaz de tomar en cuenta estos efectos, siempre y cuando, se coloque una distribución suficiente de elementos tipo viga para que las cargas aplicadas sean distribuidas a todos los nodos en el área de la losa del puente. La rigidez torsional total de la superestructura se distribuye entre todos los elementos longitudinales. La distribución y caracterización de los elementos transversales tienen, como regla general, el siguiente procedimiento: la distribución de las vigas transversales debe hacerse colocándolas, al menos, al centro y a cuartos de la longitud entre cada claro y sus propiedades deben ser equivalentes y representar el comportamiento transversal a flexión de la superestructura.
Se puede obtener un incremento en la rigidez transversal en lugares donde se presenten diafragmas en la superestructura, estos diafragmas se modelan con una retícula de vigas con características derivadas de secciones T o I y un ancho efectivo de la losa para cada una de ellas. Sólo en casos donde se necesite una detallada cuantificación del nivel de esfuerzos, se requerirá del empleo de elementos tipo placa; éstos elementos para modelar la superestructura son más importantes para evaluar las líneas de influencia y distribución de cargas que para evaluar la respuesta sísmica.

