3 Comments
Con el criterio MAC es posible medir la correlación o coherencia entre dos vectores modales que pueden ser entre medido y calculado, calculado y calculado, y medido con medido. En general, lo que hace el MAC es determinar la desviación mínima cuadrada de un vector modal con respecto a una línea recta. Está dado como (Ewins, 1984)
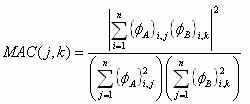
donde {
A}i,,j, { B}i,k son la coordenada del i-ésimo punto de medición de la j-ésima y de la k-ésima columna de las matrices de modos [ A] y [ B] respectivamente.
Los valores calculados con el MAC varían entre cero y uno. Valores pequeños indican baja correlación entre los vectores, mientras que valores grandes indican una correlación alta entre ellos. La aplicación del criterio MAC, al medir la correlación de un vector con respecto a otro, no se limita a formas modales, este procedimiento puede ser utilizado para comparar pares de fenómenos que poseen el mismo número de elementos que los describen.
Si el coeficiente es algún valor menor a 1.0, entonces existe un cierto grado de inconsistencia, proporcional a este valor, entre los modos. Esto puede ser causado por modelo de elementos finitos inexacto o la presencia de ruido y no-linealidades en los datos medidos. Debe hacerse notar que, para lograr un razonable grado de exactitud en la comparación, es muy importante que los puntos de medición del análisis modal coincidan con los puntos de medición en el modelo de elementos finitos.
Cabe hacer mención que se deben considerar dos casos especiales: (i) cuando los dos modos son idénticos y (ii) cuando ambos modos difieren por un mismo múltiplo escalar. Para el caso (i) se tiene: { A} º { B} , lo que resulta en MAC(A,B) = 1; y para el caso (ii) se tiene { A} = X{ B}, por lo que los dos modos están aún perfectamente correlacionados, aún tenemos que MAC(A,B) = 1.
